There is a big buzz around the whole machine learning and neural networks. But they are pretty difficult at first. So I began with where most people begin. First Machine Learning algorithm that I wrote myself, from first to last character is k Nearest Neighbor (or kNN).
For example, parametric algorithms require mathematic approach. Without it, you can have an idea how it works, but you will not be 100% sure. And I love to be 100% sure with my algorithms!
Let me give you my point of view on this algorithm! Vamos! 🙂
How kNN works
What I love about kNN is that it is very simple. There is no difficult mathematics, no derivatives. Very straightforward. If you have basic understanding of algorithms, you will understand this is no time!
Let’s go through an classification example. Our data set is in the table below. We want to know, whether (8, 5) is A or B.
| Point | Label |
| (1, 2) | A |
| (3, 5) | A |
| (12, 5) | B |
| (-1, 8) | B |
Training
If you ever have saved method’s argument to a property, you have done exactly what it takes to train kNN.
def train(self, data, labels):
self._training_data = data
self._training_labels = labels
That’s it? Yeah! 🙂
Why so easy? Because it is easy!
Predicting
When kNN makes prediction, it goes through all training examples, finds closest ones, takes majority of their labels and this is prediction.
If it sounds very harsh, do not be afraid, let me explain it in more details.
Calculating distance between two points
$$ \sqrt{ { { \sum_{i=1}^n ( a_i – b_i )^2 } } } $$
Calculating distance is only place where it takes some mathematics.
Given formula represents Euclidean distance. If it sounds scary, then don’t be! It basically means that you take difference of each coordinate, square it and take sum over all coordinates. For example, Euclidean difference between (1, 2) and (8, 5) could be calculated like this:
$$ \sqrt{ (1-8) ^ 2 + (2-5)^2 } $$
If you are more code person (I definitely am!), then below you can see the code that calculates the distance.
from math import sqrt
def _distance(self, a, b):
total = 0
for i in range(len(a)):
total += (a[i] - b[i])**2
return sqrt(total)
Picking closest targets
I believe that it would be very beneficial to calculate all distances. It will illustrate the point I want you to understand. Please notice that algorithm doesn’t necessary has to calculate all distances before weeding out some of them.
| Point | Label | Target | Distance |
| (1, 2) | A | (8, 5) | 7.616 |
| (3, 5) | A | (8, 5) | 5 |
| (12, 5) | B | (8, 5) | 4 |
| (-1, 8) | B | (8, 5) | 9.487 |
We are interested in minimal distances. This is where the k comes. The number tells us, how many distances we need.
In case of k=1, we just need one point. Our target is closest to point (12, 5) with distance 4. Can you guess prediction? 🙂
In case of k=2, we need to pick 2 closest points. They are (12, 5) and (3, 5) with respective distances 4 and 5.
In case of k=3, we pick 3 closest points (almost all data set :D). They are (12, 5), (3, 5) and (1, 2) with respective distances 4, 5 and 7.616.
And it goes on and on for every k we pick. I cannot go for more examples. I hope you see the pattern here! Carry these points to next step.
P.S. Why I cannot give you more examples? Or may I? 🙂
Choosing majority vote
Right now, when we have points that we need. We just have to pick a single label that will make our prediction.
When k=1, it is very easy! Just take label of that point and you have a prediction! In our case, algorithm predicts that (8, 5) has label B. Yay, our first prediction! 🙂
When k>1, you have to find out what labels majority of points have.
In our case, when k=3, we have three labels: B, A, A. Most of them are A, so our prediction is A.
When k=2, our labels are B and A. Which one to pick? I like to pick closer one. So I say B, but A can be predicted using other strategy. It is not set in stone here.
How it worked out?
I tried this algorithm with CIFAR-10 data set. For those, who are unfamiliar with it, it is a 32×32 image collection, that is split into 10 categories. It has 50k training and 10k testing examples.
All the work was done by my laptop. Most of the work was performed by my precious Intel® Core™ i7-7700HQ CPU.
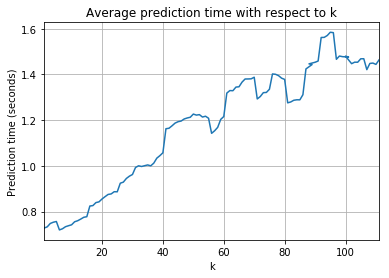
Well, it worked not as expected. My expectations were a little bit higher, but oh well. These charts sum up what had happened.
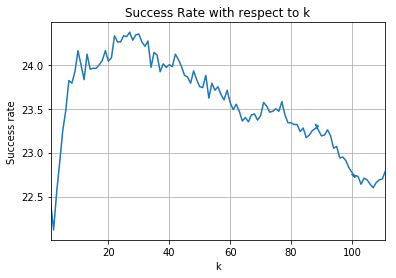
First of all, success rate is very low. This does not say that algorithm is bad – no! But it says that for this case, it is not good. The best success rate is 24.37 when k=27. I’d say that is not good enough to be used in production. 🙂
Another big point is speed. The gods of the Internet had already told me, that it is not very popular algorithm, but now I can see why. At highest accuracy, it took almost a second to calculate prediction! That is way too much. Imagine user waiting for that. Imagine thousands simultaneously. And if your case requires high k for accuracy, then you are in deep trouble!
And to finish up, this is only 50k training examples. In real world, you will probably have millions! That will take a looong as time. 🙂 Even though training is very fast, I prefer predicting to be fast.
Last words
This is how I see k-Nearest Neighbor algorithm. I am definitely not against it, it is just a tool in my toolbox. 🙂
You can always check how my working implementation looks like. I know it is not the best or fastest implementation, but it is what I wrote. It is very straightforward and great place to start with machine learning! I take pride in my work. 🙂
Do you agree with my ideas? Maybe I oversee it somehow and there is more to it?